Lucas
REDING

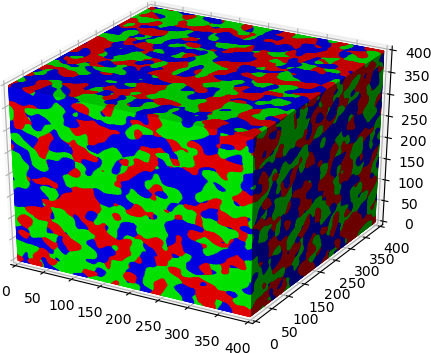
Géométrie Stochastique : Ensemble d'excursion

• Courbures de Lipschitz-Killing moyennes
• Champs aléatoires gaussiens

Mots clés : champ aléatoire, champ aléatoire gaussien, fonction aléatoire, fonctionnelles de Minkowski, courbures de Lipschitz-Killing

Résumé : On s'intéresse à la géométrie des phases apparaissant dans un modèle d'excursion de champ gaussien multivarié sur des espaces stratifiés. En supposant que le champ gaussien et l'espace stratifié sous-jacent sont tous deux suffisamment réguliers, les phases du modèle possèdent une bonne régularité et permettent d'entreprendre des calculs de géométrie stochastique. S'intéressant plus particulièrement aux courbures moyennes des phases, on peut mentionner le résultat d'Adler et Taylor (2007) donnant les courbures de Lipschitz-Killing moyennes d'un ensemble d'excursion d'un champ gaussien. Nous sommes cependant intéressés par les mesures de courbure de Lipschitz-Killing moyennes des différentes phases les unes par rapport aux autres. L'obtention de valeurs moyennes pour ces quantités nous permettrait une meilleure compréhension de la géométrie de la micro-structure des matériaux obtenus par frittage tels que les céramiques. Au travers de cet axe de recherche, nous développons aussi un module Python de manipulation et de calcul des courbures de Lipschitz-Killing sur des espaces stratifiés permettant de simplifier l'étude de tels objets.

Statistique : Estimation non-paramétrique

• Estimation de la densité et de la régression
• Estimation récursive
• Méthode des noyaux
• Normalité asymptotique - Méthode de Lindeberg

Mots clés : estimateur à noyau, estimateur récursif, estimateur de la régression, champ de variables aléatoires, normalité asymptotique, erreur quadratique moyenne, mélange fort, dépendance faible, mesure de dépendance physique, m-dépendance, méthode de Lindeberg

Résumé : Dans ce thème de recherche, nous nous intéressons aux propriétés asymptotiques d'estimateurs à noyau pour des données spatiales acquises dans une région finie d’une grille d-dimensionnelle. Nous cherchons à estimer la densité de ces données supposés être identiquement distribuées mais non nécessairement indépendantes. Nous nous intéressons aussi à la question de la régression non-linéaire sous des hypothèses de dépendance similaire. Avec l'avènement de l'informatique, la quantité de données disponibles pour le traitement s'est accrue considérablement ce qui a nécessité le développement d'estimateurs plus performants en terme de calcul : ce sont les estimateurs récursifs de la densité et de la régression. L'étude des propriétés asymptotiques de ceux-ci fait aussi partie de cet axe de recherche.

Probabilités : Théorèmes limites

• Théorèmes Centraux Limite (TCL)
• Théorèmes Centraux Limite Fonctionnels / Principe d'invariance
• Théorèmes Quenched
• Approximations par ortho-martingale

Mots clés : champs de variables aléatoires, théorème central limite quenched, théorème central limite fonctionnel quenched, approximation par ortho-martingale, condition projective

Résumé : Un problème intéressant, avec de nombreuses applications notamment en mécanique statistique, est celui de l’étude des théorèmes limite pour des processus démarrés à un point fixe. Ce problème est d’autant plus difficile que l’on perd la propriété de stationnarité dès que l’on fixe le point de départ du processus. De plus, comme le montre le contre-exemple formulé par Volný et Woodroofe (2010), l’existence d’un théorème limite « annealed » n’est pas suffisante pour affirmer la convergence en loi du processus démarré à un point fixé. Lorsqu’il y a convergence en loi du processus pour presque toutes les trajectoires passées, on parle de théorème limite conditionnel presque sûr ou théorème limite « quenched ». La question du TCL « quenched » a déjà été étudiée en détails ces dernières années cependant de nombreuses questions restent ouvertes à ce sujet.

Lien vers mon site personnel : https://sites.google.com/view/lucas-reding/